深度模型中的优化——momentum|AdaGrad|RMSProp|Adam

在随机梯度下降中，沿着最速下降方向可以得到最快的下降速度：$x_{t+1}=x_t-\lambda \triangledown f(x_t)$。其中，$\lambda$是下降步长，也被称为学习率。

在常见的SGD算法中，批量梯度下降(BSGD)的算法如下：(引用《深度学习》(花书)P₁₈₀)

算法：随机梯度下降(SGD)在第$k$个训练迭代的更新

---

Require: 学习率 $\epsilon_k$

Require: 初始参数 $\theta$

while 停止准则未满足 do

从训练集中采样$m$个样本${x^{(1)},\dots,x^{(m)}}$，其中$x^{(i)}$对应的目标为$y^{(i)}$

计算梯度估计: $\hat g \leftarrow +\frac{1}{m}\triangledown_\theta\sum_i{L(f(x^{(i)};\theta), y^{(i)})}$

应用更新: $\theta \leftarrow \theta - \epsilon \hat g$

end while

---

PS:花书中把学习率记为 $\epsilon$，把收敛条件记为$\lambda$.

下降步长对梯度下降的影响

一个简单的例子：给定目标函数 $f(x)=x^2$，初始点$x_0=1$，其梯度(导数)为$2x$，给定步长$\lambda=1$，根据上文的更新公式计算$x_1=x_0-\lambda \times 2$，发现$f(x_1)=f(x_0)$；继续进行下降更新，发现$x_2=1=x_0\dots$；如此反复，搜寻结果会反复在[-1, 1]之间横跳，且目标函数的值并不下降。

显然，随着训练的推进，我们应当逐渐减小下降步长。保证SGD收敛的一个充分条件是：

对于学习率/下降步长的选择设置，主要有以下两种情况：

• 设置过大，会出现剧烈的震荡，甚至完全不收敛；
• 设置过小，学习过程非常缓慢，且容易卡在一个局部最优值。

对于BSGD，一个比较有意思的现象是当训练的批次样本较多时，他更容易收敛。在本文中我们只在一维上进行搜索，因此很容易出现不收敛的现象。

学习率优化算法的衡量标准

引入额外误差(excess error) $J(\theta)-min_\theta J(\theta)$，即当前代价函数超出全局最小值的量。在凸问题中，SGD在$k$步迭代之后的额外误差量级为$O(\frac{1}{\sqrt{k}})$，强凸情况下是$\frac{1}{k}$。

SGD学习率的提升方案

我们以$f(x)=\sin(x)+x^2$为例子，先看看它的图像和梯度：(约定本文中所有的图横轴为迭代次数、纵轴为代价)

​x
import numpy as np
import matplotlib.pyplot as plt
​
​
def func(x):
    return np.sin(x) + np.power(x, 2)
​
​
def grad(x):
    return np.cos(x) + 2 * x
​
​
xes = np.arange(-5, 5, 0.1)
plt.plot(xes, func(xes), label="f(x)=sin(x)+x^2")
plt.plot(xes, [0 for i in xes], '--')
plt.plot(xes, grad(xes), label="f'(x)=cos(x)+2*x")
plt.legend()
plt.show()

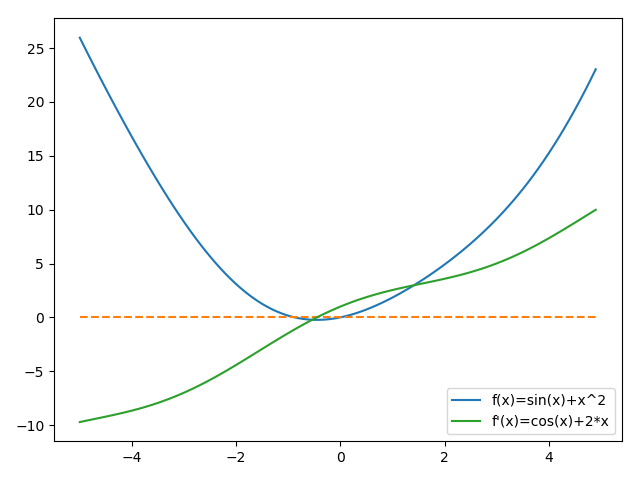
线性衰减学习率

根据SGD的收敛充分条件，我们不难给定一个线性衰减的学习率$\alpha=\frac{k}{\tau}$，设定经过$\tau$次迭代之后，令$\epsilon$保持常数。既有：

通常，设定$\epsilon_\tau$为$\epsilon_0$的$1\%$左右(令$\tau=100$）,即：$\epsilon_k=(1-0.99\mathop{\alpha}\limits_{0\to1})\epsilon_0$；但$\epsilon_0$的设定依旧容易带来函数收敛过程剧烈震荡或收敛过慢的问题，因此有更多优秀的自自适学习率算法被提出，在深度学习框架中有时把这些算法称为优化器。

利用$x_{t+1}=x_t-\lambda \triangledown f(x_t)$进行定步长SDG和衰减学习率的下降：

xxxxxxxxxx
epsilon = 1e-1  # 停止准则
lambda0 = 0.1  # 学习率(定长模式下如果给定较大的学习率可能不收敛)
x0, x1 = -150, 100
costs = []
while abs(x1 - x0) >= epsilon:
    costs.append(func(x0))
    
    temp = x1
    x1 = x0 - lambda0 * grad(x0)
    x0 = temp
print("x* = ", x0)
plt.plot(range(min(len(costs), 30)), costs[0:30], label="sgd")
​
​
epsilon = 1e-1  # 停止准则
tau, k = 100, 1
lambda0 = 1  # 学习率(可以直接给定一个较大的学习率也能保证收敛)
lambda_tau = lambda0 / tau
x0, x1 = -150, 100
costs, l0 = [], lambda0
while abs(x1 - x0) >= epsilon:
    costs.append(func(x0))
​
    temp = x1
    x1 = x0 - l0 * grad(x0)
    x0 = temp
​
    alpha = min(k/tau, 1)
    l0 = (1-alpha)*lambda0 + alpha*lambda_tau # 进行衰减
    k += 1
print("x* = ", x0)
plt.plot(range(min(len(costs), 30)), costs[0:30], label="sgd-decay")
​
plt.legend()
plt.show()

其函数图像如下(可以明显看到衰减学习率方案收敛得更快，但由于给定了大学习率，因此震荡更剧烈)：

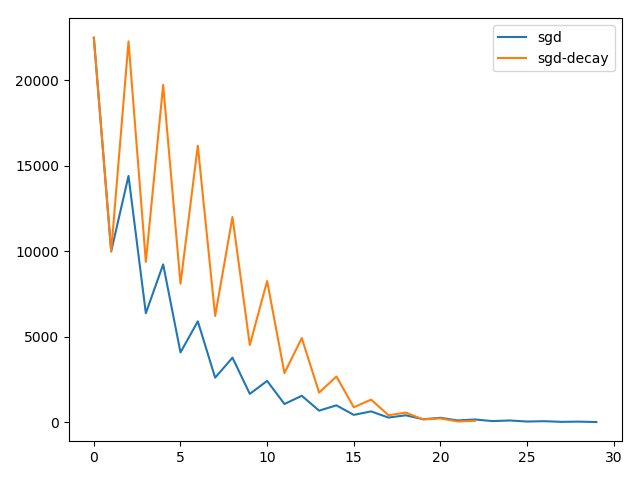
动量下降(momentum)

动量下降中引入了物理中惯性的概念，就像一个小球从山坡上滚下时，由于惯性的原因会直接冲过一些小坑，然后滚到山脚。在动量下降方案中，各超参数的更新规则如下：

算法：使用了动量下降方案的SGD

---

Require: 学习率$\epsilon$、动量参数$\alpha$

Require: 初始参数$\theta$、初始速度$v$

while 没有达到停止准则 do

从训练集中采样$m$个样本${x^{(1)},\dots,x^{(m)}}$，其中$x^{(i)}$对应的目标为$y^{(i)}$

计算梯度估计: $g \leftarrow +\frac{1}{m}\triangledown_\theta\sum_i{L(f(x^{(i)};\theta), y^{(i)})}$

计算速度更新: $v \leftarrow \alpha v - \epsilon g$

应用更新: $\theta \leftarrow \theta + v$

end while

---

直观上理解，如果梯度的方向始终一致，那么SGD就会在这个方向上不停加速，将原步长每次放大为上一轮的$1-\alpha$倍。否则，会产生一个相反的惩罚：

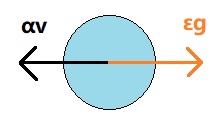
这样的好处就在于我们能够在一定情况下冲破局部最优点的陷阱，同时，面对较高的壁垒时比定步长SGD有更好的收敛性质。

在实践中，$\alpha$的取值一般为$0.5,0.9,0.99$。利用python实现：

xxxxxxxxxx
epsilon = 1e-1  # 停止准则
lambda0 = 0.5  # 给定与sgd相同的学习率
alpha = 0.5
v = 1 / (1-alpha)
x0, x1 = -150, 100
costs = []
while abs(x1 - x0) >= epsilon:
    costs.append(func(x0))
    
    temp = x1
    v = alpha * v - lambda0 * grad(x0)
    x1 = x0 + v
    x0 = temp
print("x* = ", x0)
plt.plot(range(min(len(costs), 50)), costs[0:50], label="momentum")
​
plt.legend()
plt.show()

对比图像其实很难看到momentum在收敛性上相比于定步长SGD并没有什么太大的优点，甚至给定较大步长时也容易不收敛：

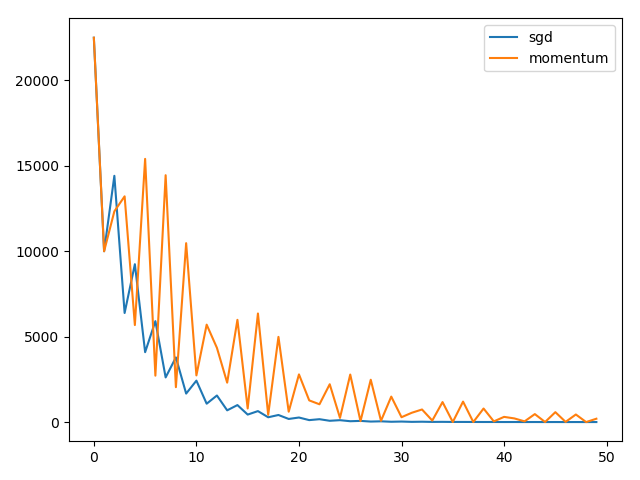
但是，如果我们稍微换一个损失函数/目标函数$f(x)=\frac{x\sin(\frac{x}{3})}{10}+\frac{x^2}{100}$，效果就会非常明显：(接下来的实验都将继续采用这个函数)

xxxxxxxxxx
def func(x):
    return 0.1 * x * np.sin(0.3 * x) + 0.01 * x ** 2
def grad(x):
    return 0.01 * np.cos(0.3 * x) * x + 0.2 * np.sin(0.3 * x) + 0.02 * x

该新目标函数的图像如下，可以看到其有多个局部最优点：

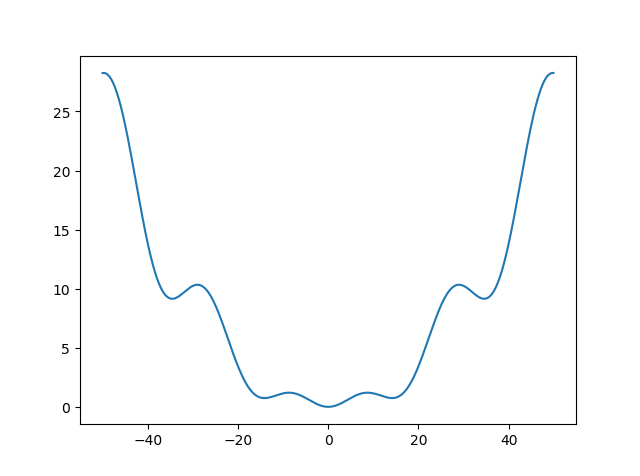
在区间$[-50,50]$中测量定步长SGD和momentum方案的性能，给定$\alpha=0.9\ ,v=0.1$、二者一致的学习率$\epsilon=0.1$：

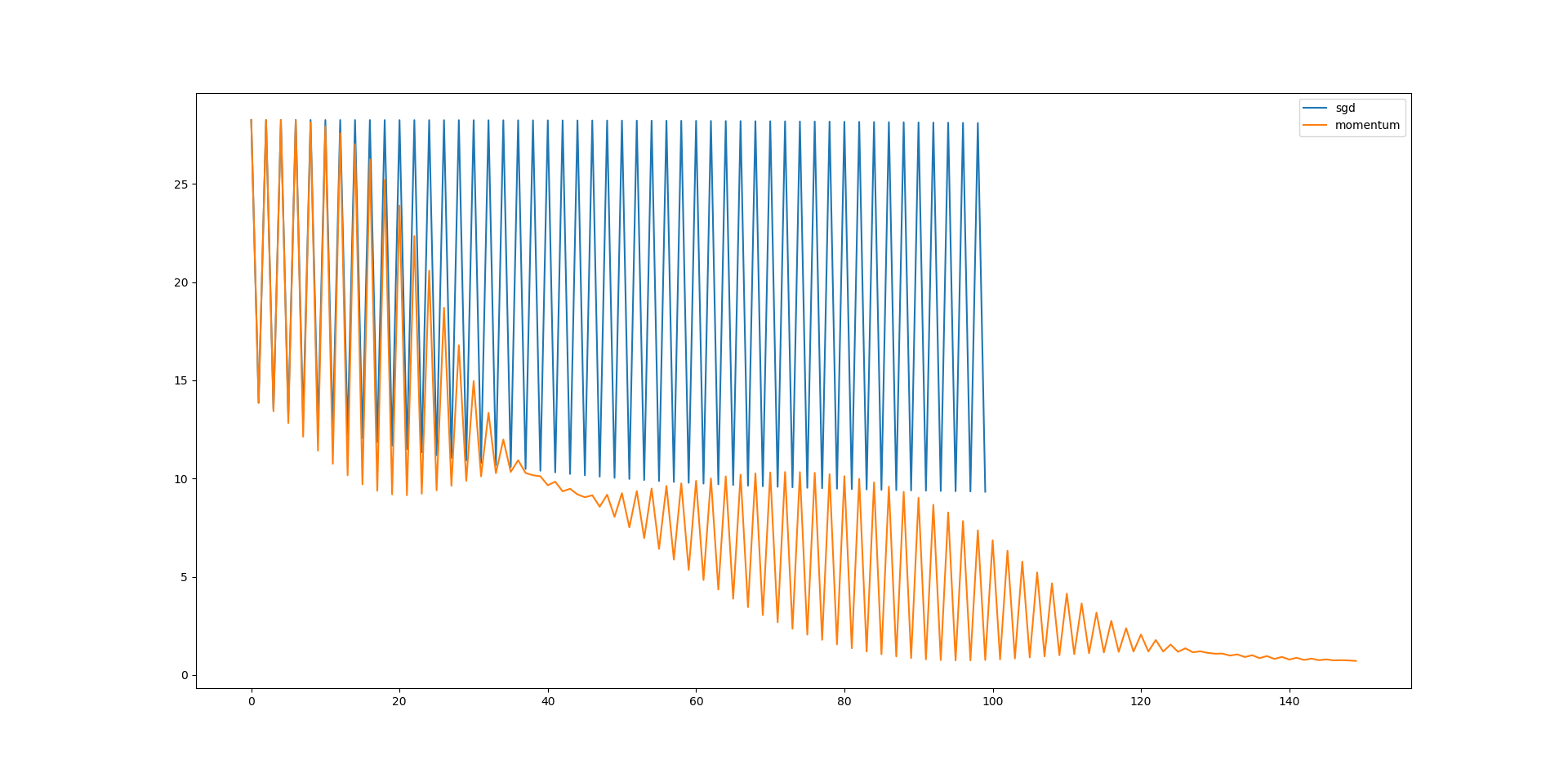
可以看到——在未经过细致调参的情况下，momentum方案冲破了第一个局部最优值$-55.36$继续下降；但是相对的，定步长SGD就没那么好运了(同样的，学习率线性衰减的SGD也会困于局部最优解)。所以，当我们提到SGD方案时，实际上往往用的是momentum及其改进方案，例如Keras框架就是这么做的。

Nesterov动量下降

为了改进momentum方案的额外误差收敛率，一个比较著名的变种是Nesterov动量下降：

算法：使用了Nesterov动量下降方案的SGD(花书P₁₈₄)

---

Require: 学习率$\epsilon$、动量参数$\alpha$

Require: 初始参数$\theta$、初始速度$v$

while 没有达到停止准则 do

从训练集中采样$m$个样本${x^{(1)},\dots,x^{(m)}}$，其中$x^{(i)}$对应的目标为$y^{(i)}$

应用临时更新: $\hat\theta \leftarrow\theta + \alpha v$

计算梯度估计: $g \leftarrow +\frac{1}{m}\triangledown_{\hat\theta}\sum_i{L(f(x^{(i)};\hat\theta), y^{(i)})}$

计算速度更新: $v \leftarrow \alpha v - \epsilon g$

应用更新: $\theta \leftarrow \theta + v$

end while

---

它将额外误差收敛率从$O(\frac{1}{k})$改进到了$O(\frac{1}{k^2})$；但是在SGD的情况下，它并没有改进收敛率。

直观上理解，Nesterov方案比momentum方案多跨了一步，即$\hat\theta \leftarrow\theta + \alpha v$，考虑得更多的是物理上的微分概念；在SGD的应用上，个人感觉并没有太大的性能改进表现，只在全批量下降时有着比较优秀的收敛性能。

AdaGrad

我们注意到，动量下降虽然在一定程度上优化了线性衰减的学习率和定步长SGD方案的弱点，但同时又引入了另一个超参数$\alpha$；而在实践中，超参数是一个非常难以确定的值。

所以我们希望学习率能在训练过程中进行自适应，即自我进行调整，以提升收敛率和降低收敛额外误差同时又不至于引入更多的超参数，减小调参的工作量。之前曾提过“成功失败法”，即Delta-bar-delta算法的变种，但缺点在于这类算法只有面对全批量下降时才比较有效。

而此处要介绍的AdaGrad算法，能够独立地适应所有模型参数的学习率，缩放每个参数反比于其所有梯度历史平方值总和的平方根。这么说可能过于拗口，我们直接看算法：

算法：AdaGrad算法(花书P₁₈₈)

---

Require: 全局学习率$\epsilon$

Require: 初始参数$\theta$

Require: 小常数$\delta=10^{-6}$(防止进行除法时的值溢出)

初始化累积变量$r=0$

while 没有达到停止准则 do

从训练集中采样$m$个样本${x^{(1)},\dots,x^{(m)}}$，其中$x^{(i)}$对应的目标为$y^{(i)}$

计算梯度估计: $g \leftarrow \frac{1}{m}\triangledown_{\theta}\sum_i{L(f(x^{(i)};\theta), y^{(i)})}$

累积平方梯度: $r \leftarrow r + g \bigodot g$

计算参数更新: $\triangle\theta = - \frac{\epsilon}{\sqrt{\delta+r}}\bigodot g$

应用更新: $\theta \leftarrow \theta + \triangle\theta$

end while

---

花书中对AdaGrad的分析较少，但作为自适应学习率算法的入门算法，我觉得有必要进行一些分析：

• 和常见的优化算法相比，AdaGrad的策略也是采取先快后慢的策略：随着算法不断迭代，$r$会越来越大，整体的学习率越来越小。
• 在凸优化问题中，由于函数总能收敛到一个最小值且AdaGrad对梯度悬崖有着很强的抑制能力，因此表现得相当不错，较少出现不收敛的情况。
• 较为直观地说，AdaGrad应用于凸优化问题时，能够给定一个巨大的学习率参数的同时保证收敛，利于加快解决优化问题时的搜寻速度。但其面对梯度壁垒时应对能力较弱，有可能被困于某个具备最优解。

xxxxxxxxxx
epsilon = 1e-1  # 停止准则
lambda0 = 100  # 学习率，AdaGrad往往需要一个极大的初始学习率
r = 0
x0, x1 = -50, -40
costs = []
while abs(x1 - x0) >= epsilon:
    costs.append(func(x0))
    g = grad(x0)
​
    temp = x1
    r =  r + g ** 2
    x1 = x0 - lambda0 / np.sqrt(1e-6 + r) * g
    x0 = temp
print("x* = ", x0)
plt.plot(range(min(len(costs), 50)), costs[0:50] label="adagrad")

得益于AdaGrad对梯度爆炸有着很好的抑制作用，所以实际上你可以给定一个很大的初始学习率，它在自我迭代的过程中也总能保证收敛。

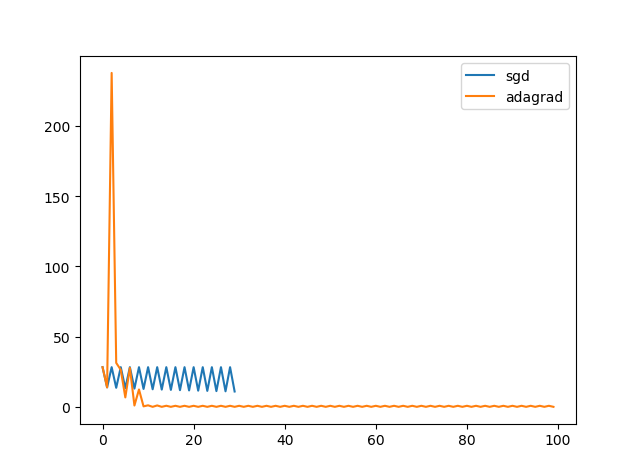
值得一说的是，AdaGrad在深度学习模型上表现得不错，比如采用64x64x1的全连接神经网络在波士顿房价回归问题上的表现如下：

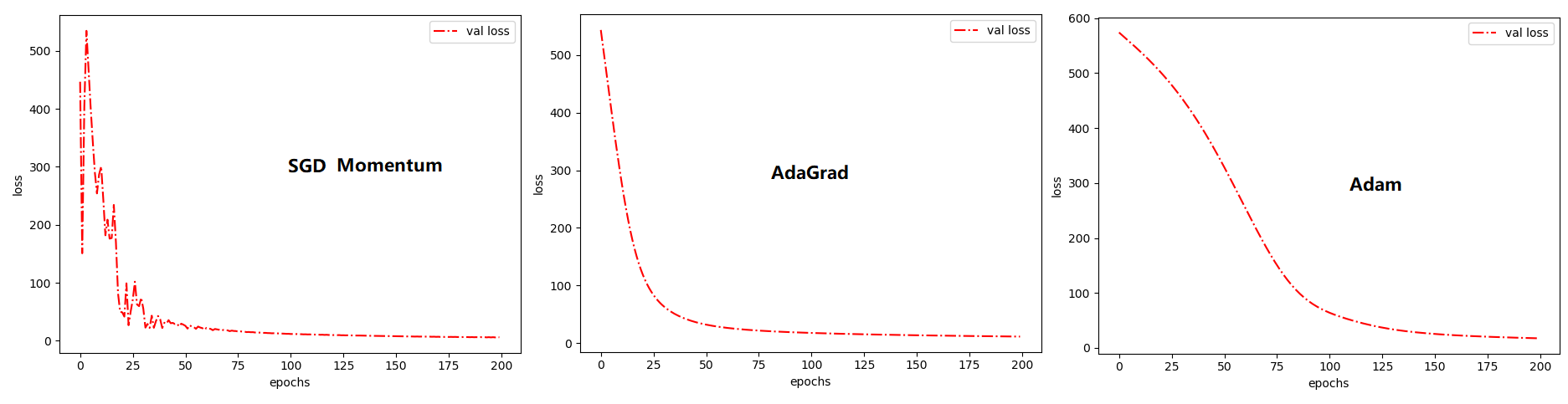
RMSProp

在上面的图像中，AdaGrad在非凸情况下表现得并不好，收敛时震荡还是比较剧烈的。同时，如果你把上文中AdaGrad的初始学习率调小，你会发现AdaGrad会跟SGD一样困于某个局部最优值。造成AdaGrad面对梯度壁垒无能为力的可能性有很多，但最大的可能是搜索在到达一个局部洼地时学习率就收缩得太小了，因此导致搜寻的脚步深陷泥沼。

因此RMSProp改变梯度累积值$r$为指数加权的移动平均值——抛弃过于遥远的历史，使其能够保证一定的跃出洼地泥沼的能力；但相对的，也会削弱其收敛率，在样本量较小时甚至完全不收敛。简单来说，就是把 $r \leftarrow r + g \bigodot g$ 改为 $r \leftarrow \rho r + (1-\rho)g \bigodot g$，其中$\rho$为衰减速率。

直观上理解，RSMProp的设计思路是这样的：梯度波动比较大的函数，它们的方差一定是非常大的，因此直接用梯度除以其二阶矩的开方，从而抑制了搜索时的摆动幅度。

算法：RMSProp算法(花书P₁₈₈)

---

Require: 全局学习率$\epsilon$、衰减速率$\rho$

Require: 初始参数$\theta$

Require: 小常数$\delta=10^{-6}$(防止进行除法时的值溢出)

初始化累积变量$r=0$

while 没有达到停止准则 do

从训练集中采样$m$个样本${x^{(1)},\dots,x^{(m)}}$，其中$x^{(i)}$对应的目标为$y^{(i)}$

计算梯度估计: $g \leftarrow \frac{1}{m}\triangledown_{\theta}\sum_i{L(f(x^{(i)};\theta), y^{(i)})}$

累积平方梯度: $r \leftarrow \rho r + (1-\rho)g \bigodot g$

计算参数更新: $\triangle\theta = - \frac{\epsilon}{\sqrt{\delta+r}}\bigodot g$

应用更新: $\theta \leftarrow \theta + \triangle\theta$

end while

---

xxxxxxxxxx
epsilon = 1e-1  # 停止准则
lambda0 = 10  # 学习率，给定一个相比于AdaGrad的学习率，其也能快速收敛和突破梯度壁垒
r, rho = 0, 0.5
x0, x1 = -50, -40
​
costs = []
while len(costs) < 1000 and abs(x1 - x0) >= epsilon:
    costs.append(func(x0))
    g = grad(x0)
​
    temp = x1
    r = rho * r + (1-rho)*g ** 2
    x1 = x0 - lambda0 / np.sqrt(1e-6 + r) * g
    x0 = temp
​
print("x* = ", x0)
​
plt.plot(range(min(len(costs), 100)), costs[0:100], label="RMSProp")
​
plt.legend()
plt.show()

运行结果如下：

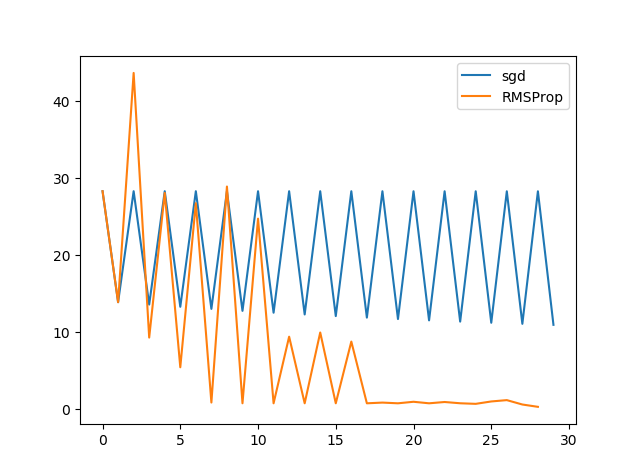
有时候，还会为其加上Nesterov动量，使得其在某些问题上具有更好的性质：

算法：使用Nesterov动量的RMSProp算法(花书P₁₈₉)

---

Require: 全局学习率$\epsilon$、衰减速率$\rho$、动量系数$\alpha$

Require: 初始参数$\theta$、初始速度$v

Require: 小常数$\delta=10^{-6}$(防止进行除法时的值溢出)

初始化累积变量$r=0$

while 没有达到停止准则 do

从训练集中采样$m$个样本${x^{(1)},\dots,x^{(m)}}$，其中$x^{(i)}$对应的目标为$y^{(i)}$

计算临时更新: $\hat \theta \leftarrow \theta + \alpha v$

计算梯度估计: $g \leftarrow \frac{1}{m}\triangledown_{\hat\theta}\sum_i{L(f(x^{(i)};\hat \theta), y^{(i)})}$

累积平方梯度: $r \leftarrow \rho r + (1-\rho)g \bigodot g$

计算参数更新: $v = \alpha v- \frac{\epsilon}{\sqrt{\delta+r}}\bigodot g$

应用更新: $\theta \leftarrow \theta + v$

end while

---

我平常在应用时，并没有觉得二者有什么特别大的差别，因此老老实实用RMSProp就行了，还能少计算一些参数和引入超参数。可能对于一些较为疯狂的调参侠而言加了Nesterov，给了他们更多的微调空间。

Adam

Adam的词源来自adaptive moments，显然这又是一种动量方案和RMSProp的变种算法。从个人经验上来看，Adam往往更加地Robust，算是我用得比较多的一种优化方案。

算法：Adam算法(花书P₁₈₉)

---

Require: 全局学习率$\epsilon=0.001$

Require: 矩估计的指数衰减速率$\rho_1,\rho_2\in[0,1)]$(建议默认0.9和0.9999)

Require: 初始参数$\theta$

Require: 小常数$\delta=10^{-8}$(防止进行除法时的值溢出)

初始化时间序列$t=0$、一阶和二阶矩变量$s=0,r=0$

while 没有达到停止准则 do

$t \leftarrow t +1$

从训练集中采样$m$个样本${x^{(1)},\dots,x^{(m)}}$，其中$x^{(i)}$对应的目标为$y^{(i)}$

计算梯度估计: $g \leftarrow \frac{1}{m}\triangledown_{\theta}\sum_i{L(f(x^{(i)};\theta), y^{(i)})}$

更新一阶矩估计: $s \leftarrow \rho_1s+(1-\rho_1)g$

更新二阶矩估计: $r \leftarrow \rho_2r + (1-\rho_2)g \bigodot g$

修正一阶矩偏差: $\hat s \leftarrow \frac{s}{1-\rho^t_1}$

修正二阶矩偏差: $\hat r \leftarrow \frac{r}{1-\rho^t_2}$

计算参数更新: $\triangle\theta = -\epsilon \frac{\hat s}{\sqrt{\hat r}+\delta}$

应用更新: $\theta \leftarrow \theta + \triangle\theta$

end while

---

观察这个算法，一阶矩和二阶矩可以简单理解成均值和方差，由于二者初始值都是$0$，因此需要在刚开始时进行放大修正防止其向$0$偏置。最后计算参数更新时，实际上用了一阶矩和二阶矩进行了估算。

矩估计可以看我的另外一篇文章：数理知识:参数估计——点估计、区间估计及置信区间

在吴恩达的公开课中，他给出他对Adam的理解，他认为Adam是momentum和RMSProp的一种结合：若把一个优化问题看成超空间上的谷地，搜索过程会在某个方向上来回摇摆，我们把这个方向记为纵轴；相反的，直达谷底的方向即为横轴。我们要做的就是抑制纵轴上的移动距离、加大在横轴上的移动距离。Adam和momentum对梯度的均值进行估计，使得纵轴上的摆动幅度减小；而对二阶矩即方差的抑制，可以进一步减小摇摆，相对的就是加大了横向搜索距离。

常用方案的对比总结

这里再快速回顾一下以上各种算法的特点。